juliatimings
This documents the timings of a simple newton method in R, C (technically cpp but it’s all just C code), and julia.
The function is f0(x)=ex+sin(x) so the newton update would be x←x−f0(x)f1(x)=x−ex+sin(x)ex+cos(x)
applied repeatedly. A graph of the curve is shown below. It’s already fairly linear so the function will hit the root very quickly but that’s ok.
curve(exp(x)+sin(x),-1,0)
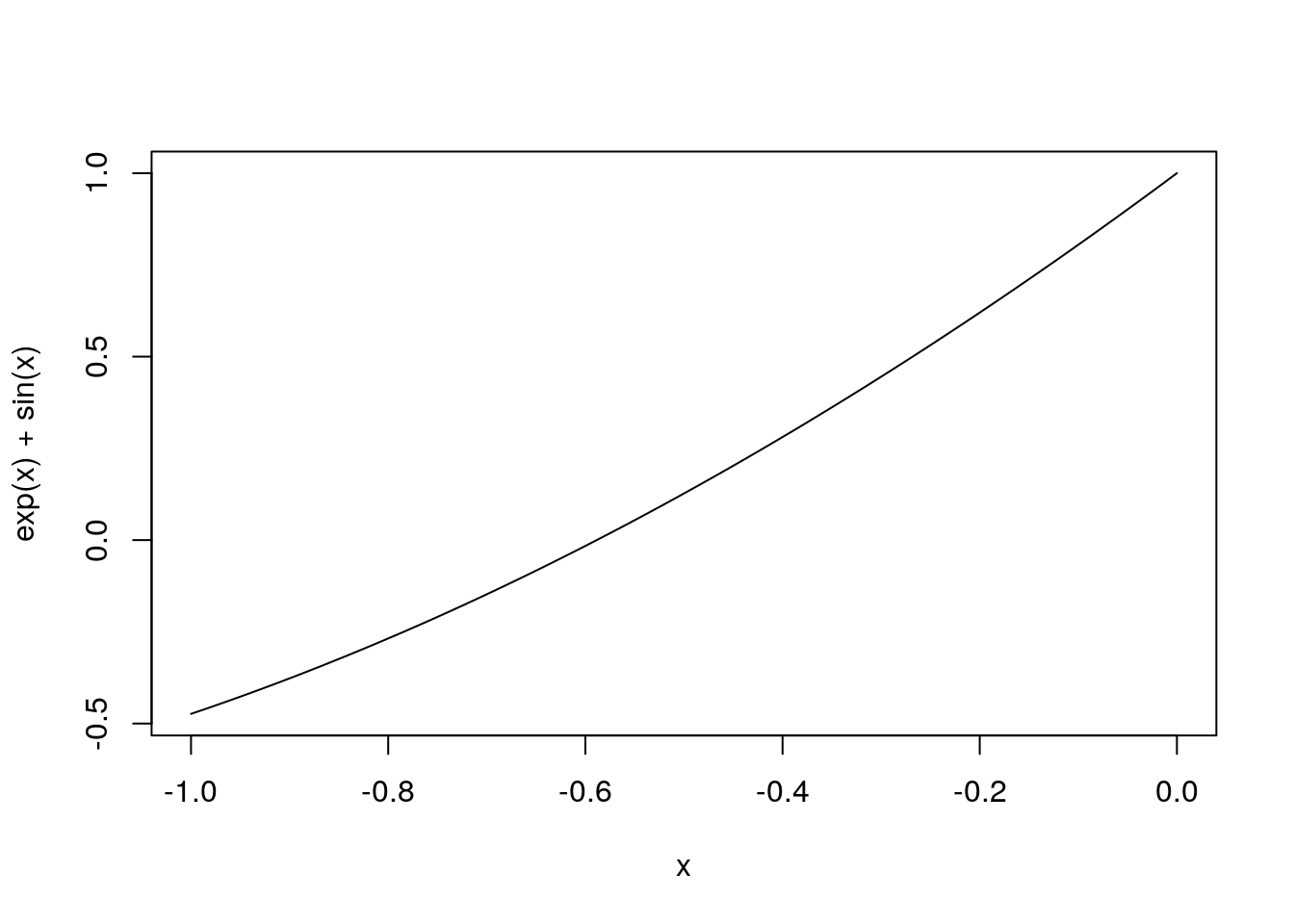 We'll run the code a fixed number of iterations. I don't know if hitting 0 in the numerator does any short-cutting in any language but thats ok for now.
We'll run the code a fixed number of iterations. I don't know if hitting 0 in the numerator does any short-cutting in any language but thats ok for now.
f0(x)=exp(x)+sin(x)
## f0 (generic function with 1 method)
f1(x)=exp(x)+cos(x)
## f1 (generic function with 1 method)
update(x)=x-f0(x)/f1(x)
## update (generic function with 1 method)
function getroot_julia()
x=0.0
for i in 1:50000
x=update(x)
end
return x
end
## getroot_julia (generic function with 1 method)
using BenchmarkTools
timing_julia = @benchmark getroot_julia() samples=5 evals=5
## BenchmarkTools.Trial:
## memory estimate: 0 bytes
## allocs estimate: 0
## --------------
## minimum time: 1.020 ms (0.00% GC)
## median time: 1.028 ms (0.00% GC)
## mean time: 1.030 ms (0.00% GC)
## maximum time: 1.044 ms (0.00% GC)
## --------------
## samples: 5
## evals/sample: 5
print(timing_julia)
## Trial(1.020 ms)
getroot_r=function(){
x=0.0
ee=0
for (i in 1:50000){
ee=exp(x)
x=x-(ee+sin(x))/(ee+cos(x))
}
return (x);
}
the c code
#include <Rcpp.h>
using namespace Rcpp;
//[[Rcpp::export]]
double getroot_cpp() {
double x=0.0;
double ee=0.0;
for(int i=0;i<50000;i++){
ee=exp(x);
x=x-(ee+sin(x))/(ee+cos(x));
}
return (x);
}
library(JuliaCall)
julia_command("f0(x)=exp(x)+sin(x)")
## Julia version 1.6.0 at location /opt/julia-1.6.0/bin will be used.
## Loading setup script for JuliaCall...
## Finish loading setup script for JuliaCall.
## f0 (generic function with 1 method)
julia_command("f1(x)=exp(x)+cos(x)")
## f1 (generic function with 1 method)
julia_command("update(x)=x-f0(x)/f1(x)")
## update (generic function with 1 method)
julia_command("function getroot_julia()
x=0.0
for i in 1:50000
x=update(x)
end
return x
end")
## getroot_julia (generic function with 1 method)
Results
Now that all the functions are created and available, they’re assessed in R. Each runs the same number of iterations with the same initial guess. Each language’s implementation is run a few times times.
library(microbenchmark)
results = microbenchmark(getroot_r(),getroot_cpp(),julia_eval("getroot_julia()"),times=5)
languages = c("R","cpp","julia")
boxplot(results,names=languages)
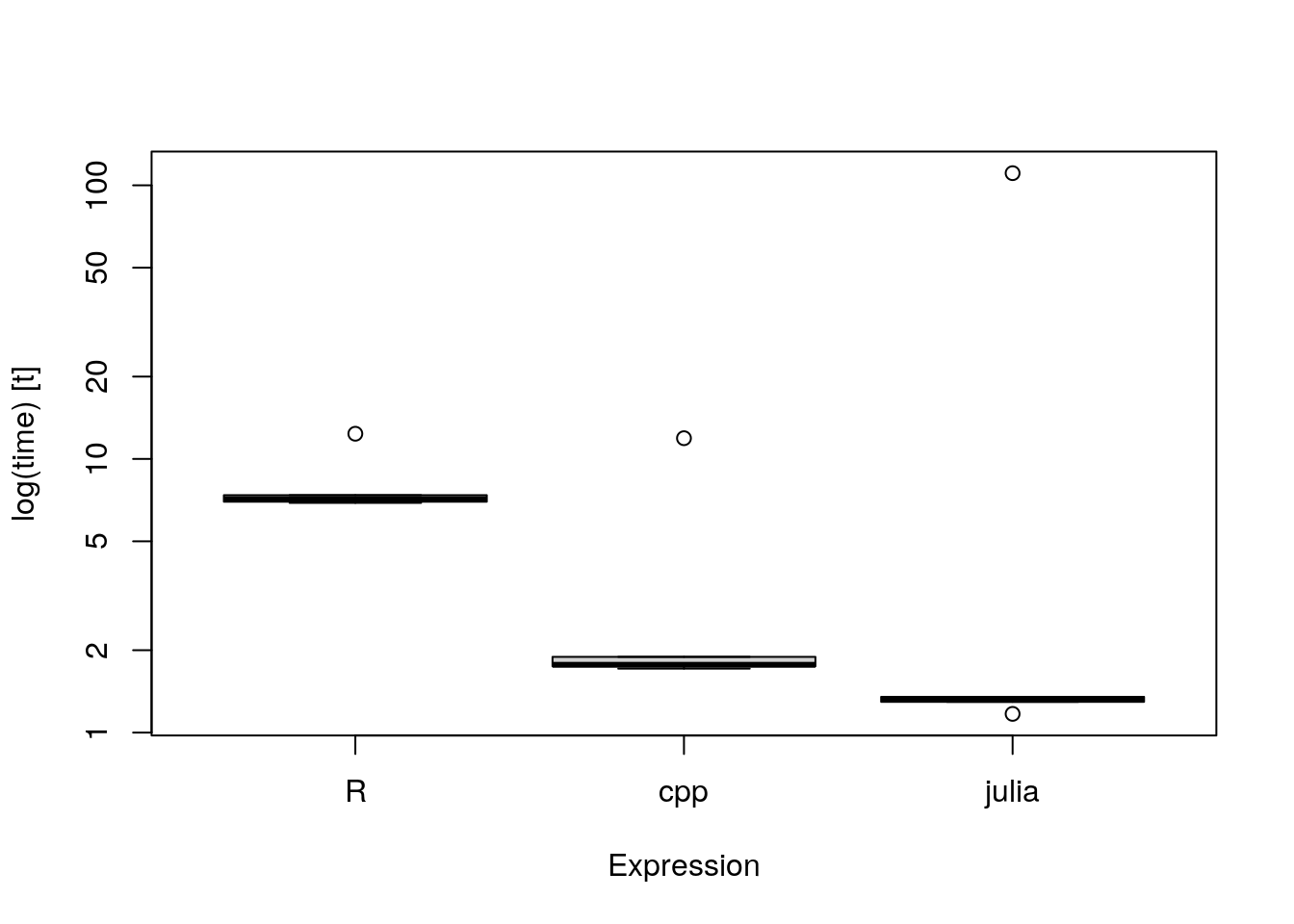
print(results)
## Unit: milliseconds
## expr min lq mean median uq
## getroot_r() 6.909239 6.978445 8.151796 7.135719 7.372746
## getroot_cpp() 1.712824 1.747627 3.805588 1.769192 1.890966
## julia_eval("getroot_julia()") 1.170483 1.295313 23.182798 1.325362 1.350895
## max neval
## 12.36283 5
## 11.90733 5
## 110.77194 5
medians = summary(results)[,"median"]
names(medians)=languages
#speeds relative to r
medians/max(medians)
## R cpp julia
## 1.0000000 0.2479347 0.1857363
#speeds relative to julia
medians/min(medians)
## R cpp julia
## 5.383977 1.334875 1.000000